Deep in the Bolivian Amazon live the Tsimane, a group of around 20 Amerindian hunter-forager communities. The tributaries and forests along the Maniqui and Quiquibey rivers provide the Tsimane with fertile lands for growing rice, yucca, plantains and maize; hunting peccaries, tapirs, monkeys and coatis; and fishing yatoramas, surubis, pirapitingas and doradas. The Tsimane produce almost all of their subsistence consumption, which also means that they are heavily exposed to extensive sources of risk and uncertainty: rain can fall out of season, crops can burn, rivers can flood, and sickness can arise.
To cope with these fluctuations in income, the Tsimane’ cannot turn to formal institutions, nor can they procure legal insurance contracts to hedge against bad times. Instead, they organize into extensive social arrangements that allow them to smooth consumption in the event of unexpected losses. These arrangements involve the transfers of goods and services across households over time. The Tsimane, as many other village communities around the world, rely heavily on informal risk sharing mechanisms, and these arrangements make up an integral part of the social fabric of these communities.
From an economic perspective, such behavior can both be rational and efficient. If the community were able to develop perfect social arrangements (contracts) to minimize risk, the consumption would vary smoothly, independently of the individual income shocks. In other words, the consumption each family would not depend on its own production but on the aggregate production of the community. However, starting in the early 90’s mounting empirical evidence suggests that risk sharing in these communities is not efficient and, even after controlling for aggregate shocks, fluctuations in individual income remains relevant to explain movements in consumption.
Several explanations have been put forth to explain inefficiencies in informal insurance arrangements such as these. For instance, the lack of commitment and enforceability, or the presence of information asymmetries, have often been suggested as principal reasons why efficiency is ruled out. However, most work has ignored the fact that risk sharing occurs bilaterally across pairs of households, and therefore that the social structure of interactions should be studied in detail as a potential impediment to full insurance.
In BSE Working Paper (No. 912), “Network-Constrained Risk Sharing in Village Economies,” Pau Milán analyzes a model of informal insurance where risk sharing occurs bilaterally along a given network of connections.
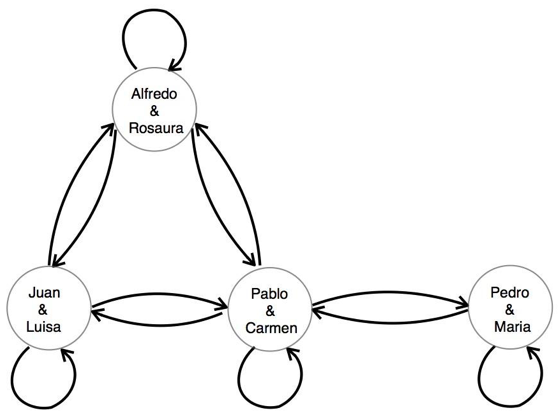
As an example, think about the community described in Figure 1. Alfredo and Rosaura have two sons, Juan and Pablo. Juan is Married to Luisa, and Pablo is married to Carmen. Carmen’s sister, Maria, also lives in town and is married to Pedro. But Pedro and Maria are not related to Juan and Luisa, nor to Alfredo and Rosaura.
Households can only share their production with the other households they are connected to. For instance, Alfredo and Maria share with their sons, and Maria share with her sister, Carmen. However, households cannot share resources with other families that they are not connected to. So, for instance, Pedro and Maria cannot share with Alfredo and Rosaura. Moreover, the model assumes that resources cannot be relayed to them through a common neighbor (in this case Pablo and Carmen). Therefore, because resources are limited in their movement along the network, the existing social structure will matter for the type of sharing that is possible.
Pau Milán characterizes constraint-efficient risk sharing in networks, and provides a number of significant implications to the empirical analysis of informal insurance. The main theoretical result fully describes the complete set of transfers across any pair of connected households, strictly as a function of their relative position in the social network. What is interesting is that the position of each family depends not only on direct, but also on all the indirect connections that it sustains.
To see this, let’s go back to the community described in Figure 1. Juan and Luisa share risk with Pablo and Carmen directly. Yet they also share their income with their parents. The larger the share of the production they give to their parents, the lower the part of the production it is available to share among them. Thereby, Juan and Luisa interact indirectly with Pablo and Carmen through Alfredo and Rosaura. Moreover, even if Alfredo and Rosaura and Juan and Luisa are not related to Pedro and Maria, they are affected by their presence because Maria receives part of Carmen’s income.
So who will get what?
It turns out that the transfers that a household receives depends on the particular identity of the families that household is connected to. This is so because, by the above argument, transfers depend not only on a family’s neighbors, but also on the neighbors of one’s neighbors, and so on and so forth along the entire network. In fact, it turns out that the appropriate way to predict transfers across families for any given network is by compiling all possible “social paths” that connect these two households with everyone else – think of “degrees of separation” as in John Guare’s famous play.
Having found the full set of efficient transfers across households, Pau Milán then draws implications for recent attempts to make sense of empirical risk-sharing results. In particular, the development literature has often modified the definition of risk-sharing groups when performing statistical tests of efficiency – for instance, by testing risk sharing along caste lines in rural India, rather than at the village level. The problem with this approach is, first, that often times it may not be obvious how to partition a particular community into sub-groups, and, secondly, that these approaches assume sub-groups (such as castes) are perfectly insured amongst themselves, but have no interaction across them. Pau Milán’s approach allows us to consider a much more general setting where local sharing groups may overlap in complicated ways along any given social structure. In fact, the partition models discussed above can be readily accommodated within the general network model defined by the author.
Moreover, Pau Milán’s model provides an economic interpretation to the existing results of empirical tests of risk-sharing. In particular, the author shows that the average response of household consumption to income can actually be decomposed into an underlying heterogeneity in responses that have to do with the varying insurance possibilities of households across the network. Moreover, he shows that these measures can be mapped into meaningful economic measures, such as consumption volatility.
Can this framework explain the food-sharing patterns in real Tsimane’ communities?
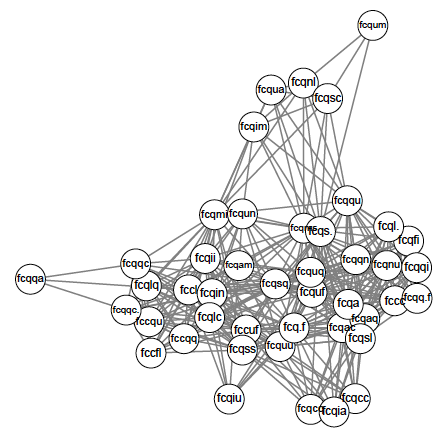
Figure 2 shows the interaction structure of one Tsimane’ village. It is orders of magnitude more complicated than the network in Figure 1, and it is therefore important to know if this behavior can be predicted from the simple theoretical predictions in the model.
To test the model, Pau Milán uses the data from the Tsimane Health and Life Story Project. From 2004 to 2009, a group of anthropologist surveyed 243 Tsimane families to gather information about the composition of the family or kinship, the time they spent in farming, and who consumed the production. This final information was transformed into a panel of production and caloric exchanges for 8 different Tsimane’ villages.
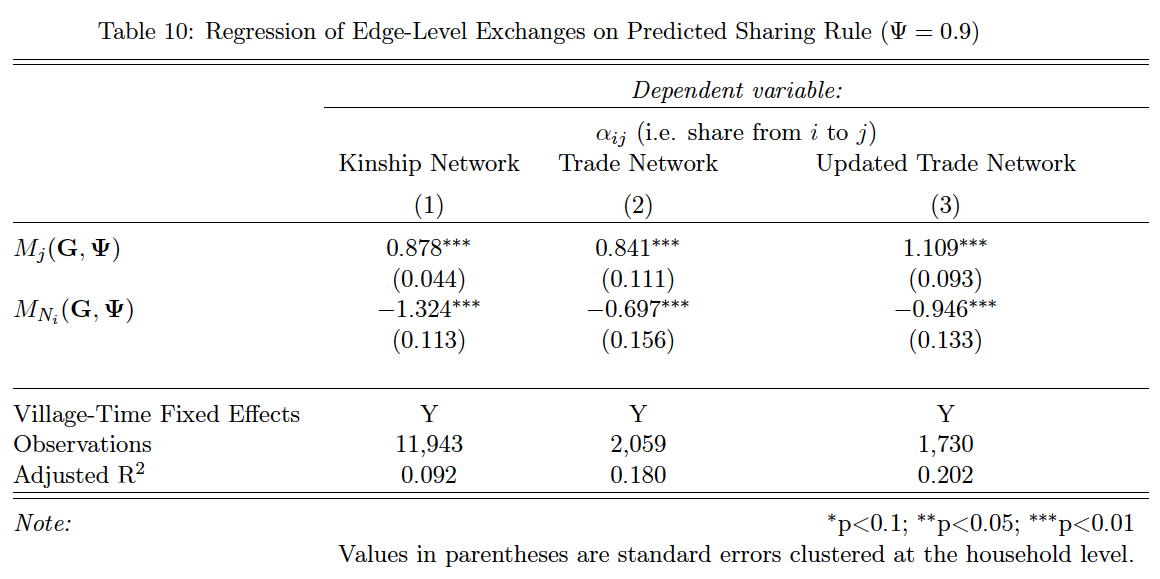
Using this unique data set, the author performs a number of empirical tests of the theory, and evaluates the implications for standard empirical results. Network structures are generated from data, for each of the 8 villages in the sample, using kinship, distance, and interaction data. The author then runs the following regression of the observed bilateral caloric exchanges that household j gives to household i (aijobs) as a function of the centrality of household j (Mj) and the centrality of the neighbors of household i (MNi):
![]()
According to the theory, if risk sharing is constrained by the network structure of the community, the share that household i receives from household j’s income depends positively on how central is j (β1 = 1) and negatively on the how central are the entire set of neighbors of i (β2 = −1). The results presented in following table are in line with such predictions.
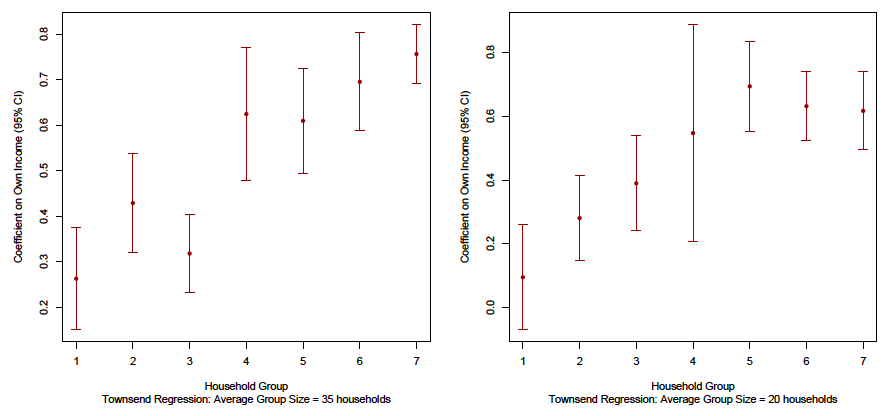
Among other tests of the theory, Pau Milán also shows that the underlying heterogeneity in consumption opportunities of households, as predicted by the theory, can be seen in the Tsimane’ data. To do this, he orders households according to the theory’s prediction on consumption response to income, splits the ordered sample into even-sized groups and then regresses consumption on income within each group – controlling for village-level shocks. The following figure shows that indeed the data exhibits the same upward trend that is predicted by the theory.
What can we learn from the Tsimane?
Overall, the evidence from Tsimane suggest that accounting for incomplete social structures explains the type of partial insurance mechanisms operating in village economies. Moreover, this theory goes beyond the mere rejection of full insurance and provides a more detailed variation on the exchanges generating consumption streams. From a policy perspective, this patterns could be used for identifying vulnerable households and determining social arrangements that would improve the welfare of the community.

