When many people disagree on the current political scenario, they might join a revolution to impose a change of regime. For this to happen, those joining the revolution must be sure that the community of revolutionaries is big and strong enough to carry out the revolution successfully. The information that people have plays a crucial role in determining this decision.
Information, indeed, is a key concept in the BSE Working Paper (No. 951), “A Model of Protests, Revolution, and Information,” by Salvador Barberà and Matthew O. Jackson. In this paper, the authors develop a model of collective action, focusing on the role of information in mass protests. The model they present is simple and flexible, and encompasses a wide variety of phenomena under a common framework. In particular, it focuses on four ways in which information can encourage or inhibit revolutions: unraveling, homophily, extremism, and counter demonstrations. The authors also discuss the role of demonstrations as a signaling device, and government’s actions in support of the status quo.
A simple coordination game
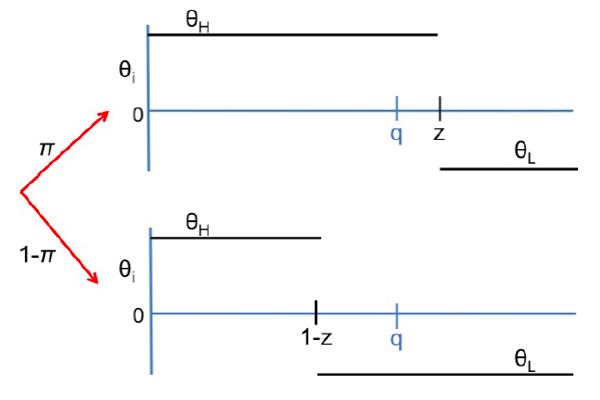
To shed light on the role of information in determining the success or failure of revolutions, let us consider first the case where, once and for all, the agents populating the economy decide whether to take part of a revolution without communicating with others. In this setting, agents can have either high desire for changing the current policy (High types), or they can be satisfied under the regulation imposed by the status quo (Low types).
The state of the world defines the number of individuals that dislike the current policy (denoted formally as z). As shown in Figure 1, the state can be either high (with probability π) or low (with probability 1-π); only in the first case, the number of revolutionaries is large enough to sustain a revolution. Agents decide whether to participate in a revolt or not based solely on their type and on the prior probability that enough people are miserable under the current regime.
The authors show that there always exists an equilibrium such that all the agents whose type is above a certain threshold participate. Then, they demonstrate that, under the assumptions of the model, revolutions are more likely to take place if the number of agents eager for change is high enough, and their beliefs of success are high. If both conditions are met, a revolution takes place and all the individuals who mistrust current policy participate in it.
Communication and the informational role of connections
The analysis becomes richer when agents can communicate among themselves. If this is the case, many different phenomena might arise due to meetings and connections.
Let us assume that everyone can meet once with another individual chosen uniformly at random. After the meeting, they update their beliefs about the size of the potential revolt, and about its likelihood of occurring. This additional information is relevant only when their prior beliefs are weak, and acts in opposite ways on the equilibria: On the one hand, when High types meet other High types, they attach a higher probability to the High state; on the other hand, H types realize that other H types (not necessarily connected with them) will meet with L types and will be discouraged to revolt, reducing the number of supporters for the revolution. The subtle point here is that agents expect little support for a revolution because many others H types will be discouraged by meeting the L types. This phenomenon is what the authors call unraveling.
An alternative to uniform meetings is that people are more connected with their similar. This is called homophily. Under homophily, connections provide less information to the learner. Homophily can have opposite effects on the equilibria of the economy, depending on the strength of agents’ prior beliefs and on the correlation of types with the state. In fact, homophily decreases the informational value of meeting, but, at the same time, reduces the number of H types discouraged by meeting with the L types. Figure 2 represents in the (z,π) space how equilibria change from a world where meetings occur uniformly to one with homophily.
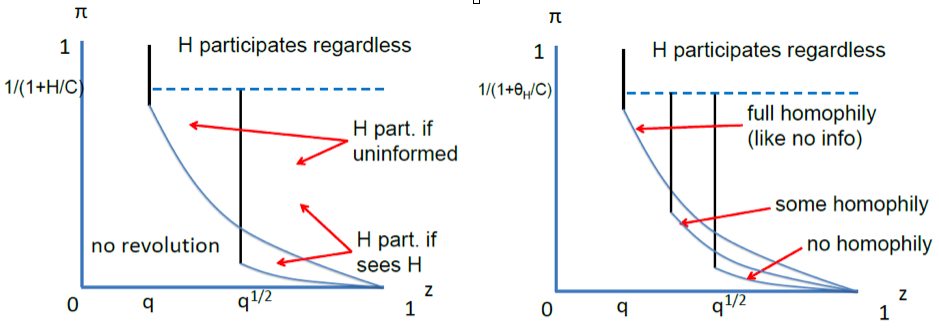
In contrast with the case where agents have only one connection, large amounts of information are always help revealing the state of the world. The authors show that, as the number of others observed increases, the fraction of H types participating in the ‘High state goes to one and the fraction of H types participating in the ‘Low state goes to zero; in this sense, the protest is perfectly effective in the limit. What happens if we introduce homophily and agents have multiple connections? Intuitively, homophily lowers the informational content of signals, so that agents need more connections to learn the true state of the economy.
Dynamics and contagion
The authors extend the static model presented before by assuming that revolutions can take place in more than one period, and in more than one country. What is the effect of demonstrations on future revolts? The authors claim that demonstrations increase the likelihood of holding a revolt in the future, if participation is costly. The reason is that demonstrations can convince moderate supporters to join future revolutions; they signal that the economy is in the ‘High state. Still, this happens only when participating in a demonstration is a costly action for the participants. Based upon this argument, the authors explain that pools and communication through social media are a sort of cheap talk communication; hence, they cannot be considered an effective tool for enhancing the chances of having revolutions.
An additional extension of the model assumes that revolts can take place in two correlated countries, with correlated states. In this case, a possible equilibrium is one in which both countries revolts. One of these countries has enough support for the revolution; the other goes in revolt as the states of both countries are correlated. This outcome describes a situation parallel to the events that led to the Arab spring: Countries that had revolts recorded also high correlation between their unemployment rates.
The study of the consequences of revolutions is complementary to all the cases previously described. If we assume that agents care about the regime imposed by the new rulers after the revolution, equilibrium outcomes change. This happens because individual with moderate preference for change might dislike extreme revolution outcomes. Agents with moderate preferences will not participate in revolutions made by many extreme individuals.
Support for the status quo: Counter demonstrations and government’s actions
We already covered extensively agents’ incentives to join a revolution. Now we shift the angle of analysis, studying government’s actions and agents’ incentives in support of the status quo. When agents can provide counter demonstrations, many diverse equilibria might occur. Most importantly, counter demonstrations can be useful for revealing the state of the world, and can be used to eventually determine the equilibria of the economy in case of moderate support.
Support for the status quo can also come from government’s actions, which can affect the cost of participating a reform in case of failure, or inform people via propaganda and redistribute wealth among them. It is interesting to point out that, for the last two actions described, it is sufficient for to convince a fraction of the population for discouraging the rest of it. Moreover, if the government wants to convince the population through redistribution, it must act in mixed strategies, since either the government or some individual would revise his play in any pure strategy equilibrium.
Conclusions
Salvador Barberà and Matthew O. Jackson presented a simple and flexible model of collective action to explain how information can create or hinder revolutions. Several extensions of the basic setup have been made by altering the way agents meet with each other and by considering two periods and two correlated countries. Interestingly, by introducing the last extension, the model becomes very insightful for explaining the course of events that lead to the Arab spring. Many interesting elements such as free-riding behavior and feedback between politics and demonstrations can be included in the model, but for this we need to wait for future contributions.


